Difference between revisions of "Robot-Camera Calibration Tool"
(Completed instructions for version 0.8b) |
(explained the error validation) |
||
| Line 21: | Line 21: | ||
# Type the position of calibration ball in robot coordinate system into the application. | # Type the position of calibration ball in robot coordinate system into the application. | ||
#* Tip: If you use a program to position the robot, it is useful to save all planned positions into a file and load it into calibrations table. Values in a row should be separated by white space, each row on the new line. | #* Tip: If you use a program to position the robot, it is useful to save all planned positions into a file and load it into calibrations table. Values in a row should be separated by white space, each row on the new line. | ||
| − | # Type the rotation of gripper into the application [ | + | # Type the rotation of gripper into the application [mandatory when rotating the gripper]. |
| − | #* This step is not necessary, but | + | #* This step is not necessary when the gripper rotation doesn't change, but in general it improves the calibration accuracy. When the ball is not exactly at the gripping point, the actual position of calibration ball slightly differs from the position reported by the robot. This '''misplacement error''' can be eliminated knowing the gripper rotation. |
#* Pick the right rotation formalism from the rotation combo box. This format is used for all points at the time of matrix computation. | #* Pick the right rotation formalism from the rotation combo box. This format is used for all points at the time of matrix computation. | ||
# Use <code>Capture</code> button to trigger new scan and locate the calibration ball. | # Use <code>Capture</code> button to trigger new scan and locate the calibration ball. | ||
| Line 29: | Line 29: | ||
===Computation=== | ===Computation=== | ||
# Hit <code>Compute</code> button. | # Hit <code>Compute</code> button. | ||
| − | # The output console shows the process of computation. | + | # The output console shows the process of computation. |
| − | # Computed matrix is displayed in the table. Save it to a file for later use. | + | #* Note: If rotation formalism was used, the output shows also computed misplacement vector that indicates the difference between the actual ball placement and the placement reported by robot. |
| − | + | # Computed transformation matrix is displayed in the table. Save it to a file for later use. | |
| + | |||
| + | ==Testing the result== | ||
| + | |||
| + | To see the result of applying the transformation on camera point, hit <code>Test</code> button. This will trigger new scan, locate calibration ball and transforms its position into robot coordinates. The output is shown in output console. This process will not consider the gripper rotation, because in real case scenario the misplacement vector changes with every picked object. | ||
| + | |||
| + | ===Validating the transformation accuracy after computation=== | ||
| + | |||
| + | In this scenario, we put the calibration ball inside the gripper, collected calibration points and ran computation of calibration matrix. We did not moved the calibration ball. To validate the transformation accuracy, we will go through the same robot positions and compare them with values calculated by <code>Test</code> button. | ||
| + | |||
| + | # The first testing position in robot space is '''[0, -600, 100]''' and the rotation of gripper expressed as rotation vector is '''[3.14159, 0, 0]'''. | ||
| + | # The misplacement vector of our computation was: '''[-0.0422, -8.0056, 4.4710]''' (this information is shown in output console after computation the transformation matrix) | ||
| + | # We put the robot in first testing position and hit <code>Test</code> button: | ||
| + | #* Calculated ball position in robot space was '''[-0.435708, -592.207, 95.3183]'''. | ||
| + | #* We add misplacement vector to calculated position, the resulting point is '''[-0.47791, -600.213, 99.7893]''' (misplacement vector should be added according to the gripper rotation. In this example, we simply summed the X,Y,Z values) | ||
| + | #* The transformation accuracy is thus less than 0.6 mm. | ||
Revision as of 18:08, 13 January 2017
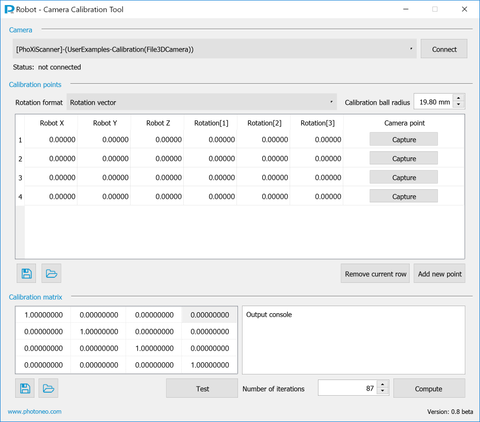
Robot-Camera Calibration Tool is used to find the transformation between the camera (PhoXi 3D Scanner) and robot coordinate spaces. Computed matrix transforms points from camera coordinate system to robot coordinate system.
You need a licensed USB Dongle to run the application.
Contents
Calibration process
Preparation
- Mount robot and camera so as their mutual position is fixed.
- Get calibration ball. This might be a table tennis ball or a bearing ball. (When using bearing ball make sure it is not too shiny so the scanner can locate it with high accuracy.)
- Put the calibration ball into the robot's gripper at the gripping point.
- Start PhoXi Control Application.
- Plug in your licensed USB Dongle.
- Start Robot-Camera Calibration Tool, select desired 3D PhoXi Scanner and hit
Connectbutton. - Set the radius of calibration ball in the application. This value is used for locating the calibration ball in captured 3D scans.
Collecting calibration points
- Move the gripper with the ball in front of the camera.
- Choose a representative location, e.g. when calibrating for bin-picking application, the locations should cover the area where desired objects will be picked.
- Type the position of calibration ball in robot coordinate system into the application.
- Tip: If you use a program to position the robot, it is useful to save all planned positions into a file and load it into calibrations table. Values in a row should be separated by white space, each row on the new line.
- Type the rotation of gripper into the application [mandatory when rotating the gripper].
- This step is not necessary when the gripper rotation doesn't change, but in general it improves the calibration accuracy. When the ball is not exactly at the gripping point, the actual position of calibration ball slightly differs from the position reported by the robot. This misplacement error can be eliminated knowing the gripper rotation.
- Pick the right rotation formalism from the rotation combo box. This format is used for all points at the time of matrix computation.
- Use
Capturebutton to trigger new scan and locate the calibration ball. - Repeat until sufficient number of calibration points are collected. The minimum is 4 points.
Computation
- Hit
Computebutton. - The output console shows the process of computation.
- Note: If rotation formalism was used, the output shows also computed misplacement vector that indicates the difference between the actual ball placement and the placement reported by robot.
- Computed transformation matrix is displayed in the table. Save it to a file for later use.
Testing the result
To see the result of applying the transformation on camera point, hit Test button. This will trigger new scan, locate calibration ball and transforms its position into robot coordinates. The output is shown in output console. This process will not consider the gripper rotation, because in real case scenario the misplacement vector changes with every picked object.
Validating the transformation accuracy after computation
In this scenario, we put the calibration ball inside the gripper, collected calibration points and ran computation of calibration matrix. We did not moved the calibration ball. To validate the transformation accuracy, we will go through the same robot positions and compare them with values calculated by Test button.
- The first testing position in robot space is [0, -600, 100] and the rotation of gripper expressed as rotation vector is [3.14159, 0, 0].
- The misplacement vector of our computation was: [-0.0422, -8.0056, 4.4710] (this information is shown in output console after computation the transformation matrix)
- We put the robot in first testing position and hit
Testbutton:- Calculated ball position in robot space was [-0.435708, -592.207, 95.3183].
- We add misplacement vector to calculated position, the resulting point is [-0.47791, -600.213, 99.7893] (misplacement vector should be added according to the gripper rotation. In this example, we simply summed the X,Y,Z values)
- The transformation accuracy is thus less than 0.6 mm.